円周上でランダムにとった3点でつくられる三角形が鋭角三角形になる確率は、1/4ということであった。
以前の結果を使って結論を出したが、この「円周上のランダムな3点による三角形が鋭角三角形になる確率」の求め方について、改めて整理しておこう。
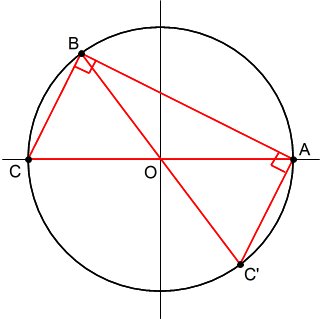
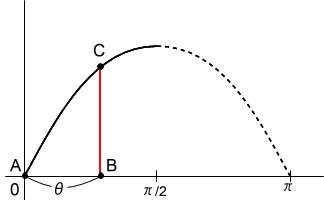
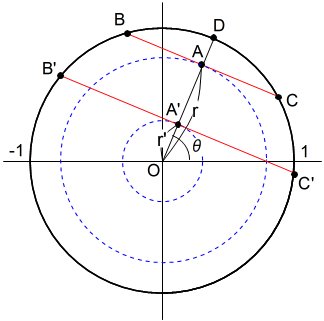
中心が原点にある単位円に、3点A,B,Cをとって三角形を描く。
点Aは、座標(1,0)に固定する。
点Bは、上半円周の任意の点とし、弧AB=a とする。
点Cは、円周上の任意の点とし、弧ABC=b とする。
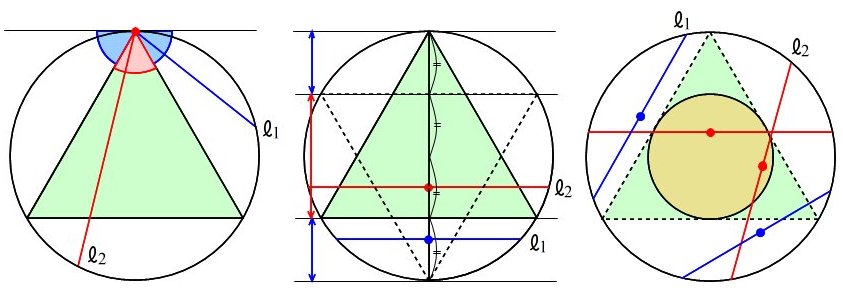
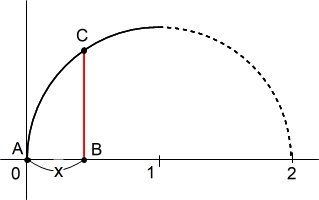
点Bが、0<a<π のとき、点Cが、π<b<π+a を満たせば(赤色の弧の上にあれば)、鋭角三角形になる。
赤色の弧の長さは、弧ABの長さ(a)と同じなので、鋭角三角形になる確率は、a/(2π) となる。
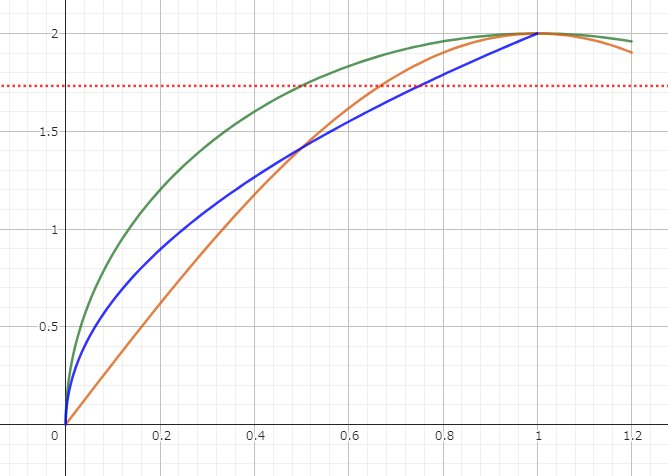
この a が 0からπまで変化するときの f(a)=a/(2π) が全体のどれだけの割合になるかを調べればよい。
f(a)=a/(2π) を(0→π)で積分して、πで割る(青色の面積を底辺で割る)ことで、
{[(1/(4π))a^2](0→π)}÷π=(π/4)÷π=1/4 すなわち、確率 1/4 (=0.25)が得られる。
新たに条件を加えて、次のような問題をつくってみた。
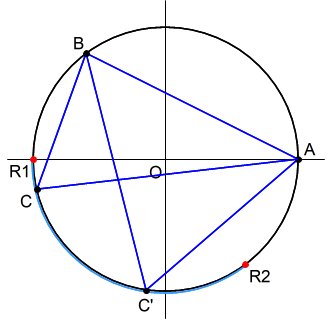
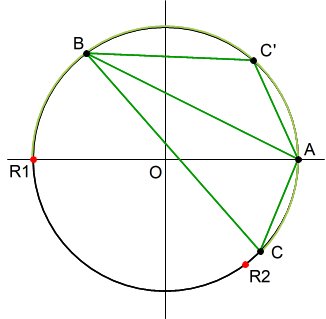
点A,Bは上記と同じとし、点Cは、「弧ABを除く円周上に配置する」こととする。この場合、「鋭角三角形になる確率」はいくらか。
上記と同じく、点Cが、π<b<π+a を満たせば(青色のエリアにあれば)よいわけだが、点Cを弧AB上(赤色のエリア)に置いてはいけないので、鋭角三角形になる確率は、a/(2π-a) と表せる。
すなわち、 f(a)=a/(2π-a) の積分から確率を求めることになる。
2π-a=x とおいて置換積分すると、(x-2π)/x を(2π→π)で積分することになり、[x- 2πlogx](2π→π)= 2π log 2-π ≒ 1.212
これを π で割ればよいので、求める確率は、2 log 2-1 ≒ 0.386 となる。